MATEMATICAS
👆SEGUNDO PERIODO👆
=================================================================================
GUIA # 3 PERIODO 1
|
GUÍA DE APRENDIZAJE N° 3 – PRIMER PERIODO |
|
|
Área: MATEMÁTICAS Asignatura: Matemáticas Grado: 10° Año: 2021 Docente: Juan Carlos Muñoz Castro Grupos: 10º 01, 10º 02, 10º 03 y
10º 04 Fecha de Inicio: 22 de marzo de 2021 Fecha Máxima de devolución: 9 de abril de
2021 |
|
|
Componente |
Espacial Métrico |
|
Tiempo |
Esta guía está diseñada para que la realices
en 3 semanas, dedicando 4 horas a
la semana |
|
Instrucciones para desarrollar la actividad |
Primero: Dedica un tiempo mínimo de una hora
cada semana a los saberes previos para su asimilación. Segundo: Dedica un tiempo mínimo de una hora
cada semana a la estructuración para su comprensión. Tercero: Dedica un tiempo mínimo de 2 horas
semanalmente a la transferencia para su desarrollo. Cuarto: Sí, tienes dudas o inquietudes en la
estructuración o en las actividades, consulta
al docente de la asignatura de tu grupo en el horario de comunicación semanal
con el docente atraves de llamada telefónica o video llamada. |
|
Recomendaciones |
Las actividades de transferencias se deben realizar en el cuaderno de
matemáticas. Al comienzo de cada actividad de transferencia debe tener el siguiente
encabezado: Nombre completo del estudiante, tema de la actividad, curso, periodo y
nombre del docente al que le envía. Si las actividades que envías no tienen
el encabezado, la actividad será devuelta. Enumera secuencialmente cada hoja
de la actividad En los videos que debas enviar debes de salir con el uniforme de
diario de la institución |
|
Medio de entrega |
Deben enviarlo al WhatsApp del docente de su grupo Juan Carlos Muñoz Castro: WhatsApp: 304 668 40 19 |
|
Productos a entregar por el estudiante |
Fotografías
de las actividades de transferencias
resuelta en el cuaderno de
matemáticas Un video donde expliques una de las actividades
de transferencias de la guía |
|
Hora de comunicación semanal con el docente |
Juan Carlos Muñoz Castro Grupo 10º 01
jueves de 7:00 a.m. a 9:00 a.m. Grupo 10º 02
miércoles de 7:00 a.m. a 9:00 a.m. Grupo 10º 03
viernes de 7:00 a.m. a 9:00 a.m. Grupo 10º 04
jueves de 9:00 a.m. a 11:00 a.m. |
Primera Semana: Triángulo
v
Saberes
Previos
Ø Triángulo: es la región del plano limitada por tres segmentos de rectas que se
intersecan dos a dos. En un triángulo se identifican los siguientes elementos:
·
Vértice: son los puntos de intersección de
cada par de segmento de rectas que forman el triángulo. Los vértices se nombran
con letras mayúsculas (A, B, C).
·
Lados: son los segmentos determinados por dos
vértices. Los lados de un triángulo se nombran con la misma letra del vértice
opuesto, en minúscula (a, b, c).
·
Ángulos Interiores: son los que forman dos
ángulos consecutivos (
Ø Propiedades de los Triángulos: todo triángulo cumple las siguientes propiedades:
·
La suma de las medidas de los
ángulos internos de un triángulo es 180º.
·
Al lado de mayor longitud se opone
el ángulo de mayor amplitud, y al lado de menor longitud se opone el ángulo de
menor amplitud.
·
La medida de cada uno de los lados
es menor que la suma de las medidas de los otros dos lados.
·
La medida de un ángulo exterior es
igual a la suma de dos ángulos interiores no adyacentes
·
Si dos lados de un triángulo son
congruentes, entonces, los ángulos opuestos a estos lados son congruentes.
Clasificación de Triángulos: los triángulos se clasifican según la medida de sus lados y según la medida de sus ángulos, así:
Ø Triángulo Rectángulo: es el que tiene un ángulo recto, es decir, un ángulo que mide 90º. En
todo triángulo rectángulo, los lados que forman el ángulo recto se llaman catetos y el ángulo opuesto al ángulo
recto se llama hipotenusa.
Ø Teorema de Pitágoras: en todo triángulo rectángulo, el cuadrado de la longitud de la
hipotenusa es igual a la suma de los cuadrados de la longitud de los catetos c2 = a2
+ b2.
v
Estructuración
Analiza la
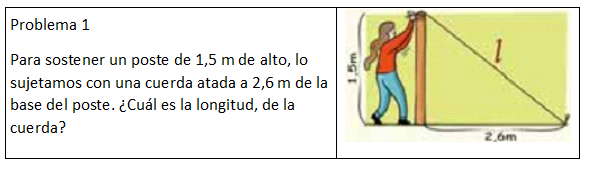
resolución del siguiente problema
Paso 1: Comprendo el
problema
·
Datos: Nos dan el valor de los dos catetos,
cateto a es 1,5 m y cateto b es 2,6 m.
·
Pregunta: ¿Cuál es la longitud de la cuerda?
Paso 2: Elabora un
plan y lo llevo a cabo
Se calcula la longitud de la cuerda usando el teorema de Pitágoras.
Como la longitud de la cuerda en el triángulo rectángulo
que se forma es la hipotenusa (c),
entonces:
R: La longitud de la cuerda es 3 m
Analiza la resolución del siguiente problema
Paso 1: Comprendo el
problema
·
Datos: Nos dan el valor de un cateto y la
hipotenusa, el cateto b es 25 dm y
la hipotenusa c es 65 dm.
·
Pregunta: ¿A qué altura se apoya la parte
superior de la escalera en la pared?
Paso 2: Elabora un
plan y lo llevo a cabo
Se calcula la altura a la cual está apoyada la escalera
en la pared usando el teorema de
Pitágoras.
Como la altura a la cual está apoyada la escalera en la
pared en el triángulo rectángulo que se forma es el cateto a, entonces:
R: La escalera está apoyada en la pared a una altura de 60 dm
v
Transferencia
Actividad 1: Resolver los siguientes problemas
Segunda Semana: Ángulo
v Saberes Previos
Ø Ángulo (
Ø Medición de Ángulos: Las unidades de medición de ángulos usadas con
mayor frecuencia son el grado y el radián. El grado es la unidad de medida del sistema
sexagesimal y el radián es la unidad de medida del sistema cíclico.
Ø Medición de Ángulos en el
Sistema Sexagesimal o en Grados: El ángulo
generado por una rotación completa, se denomina ángulo giro o de una vuelta. La medida de un ángulo giro es 360
grado y se denota 360º.
Un grado sexagesimal se
define como (1 ÷ 360) parte de la rotación total.
El grado tiene dos
submúltiplos: el minuto y el segundo.
1 minuto (1´) = (1 ÷ 60)º y
1 segundo (1”) = (1 ÷ 60)´ o también 1º = 60´ = 3.600” y 1´ = 60”
v Estructuración
Problema 1: Analiza la resolución del siguiente problema
Un avión puede despegar con un ángulo mínimo de 37,425º.
¿Cuál es el ángulo mínimo en grados, minutos y segundos?
Paso 1: Comprendo el
problema
·
Datos: La medida del ángulo es 37,425º.
·
Pregunta: ¿Cuál es el ángulo mínimo en grados,
minutos y segundos?
Paso 2: Elaboro un plan y lo llevo a cabo
|
Primero, se
descompone la medida del ángulo como la suma de su parte entera y su parte
decimal: 37,425º = 37º + 0,425º La parte decimal se multiplica
por 60´ para hallar la cantidad de minutos = 37º + (0,425 * 60´) = 37º +
25,5´ |
Luego, si existe
parte decimal en la cantidad de minutos, se repite el proceso multiplicando
por 60” así: = 37º + 25´ + 0,5” = 37º + 25´ + (0,5 * 60”) = 37º + 25´ + 30” |
Finalmente, se tiene
que el ángulo mínimo con el que despeja el avión es de 37º 25´30” |
Problema 2: Analiza
la resolución del siguiente problema
La cuerda de una cometa en vuelo forma un ángulo con la
horizontal de 43º 30´ 36”. ¿Cuál es la medida del ángulo en grados?
Paso 1: Comprendo el
problema
·
Datos: La medida del ángulo es 43º 30´ 36”.
·
Pregunta: ¿Cuál es el ángulo mínimo en grados,
minutos y segundos?
Paso 2: Elaboro un
plan y lo llevo a cabo
|
Primero, se expresa
la medida del ángulo como la suma de sus partes, convirtiendo cada una a
grados según la equivalencia 1º = 60´ = 3.600”. Así: 43º 30´ 45” = 43º + (30´ ÷
60´)*1º + (36” ÷ 3.600”)*1º = 43º + (0,5)*1º + (0,01)*1º = 43º + 0,5º + 0,01º
= 43,51º |
Finalmente, se tiene
que la cuerda de la cometa forma un ángulo de 43,51º con la horizontal. |
v Transferencia
Actividad
2: Resolver el siguiente problema
Tercera Semana: Equivalencia
Entre el Sistema Sexagesimal y el Sistema Cíclico
v Saberes Previos
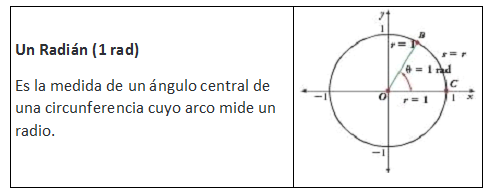
Ø Equivalencia Entre Grado y Radianes: La equivalencia entre grados y
radianes se obtiene a partir de la fórmula de la longitud de una circunferencia.
Así:
La longitud
de una circunferencia (c) = 2
El
radio de una circunferencia cabe en su perímetro exactamente 2
Esto
quiere decir que un ángulo completo cuya medida es 360º equivale a 2
|
Para determinar la equivalencia de
un grado en radianes se tiene que: 360º = 2 180º = 1º = ( 1º = ( |
Para determinar la equivalencia de
un radián en grado se tiene que: 2 1 rad = (180 ÷ 1 rad = (180º ÷ |
v Estructuración
Problema 1: Analiza
la resolución del siguiente problema
Las bisagras de una puerta de seguridad tienen una apertura
máxima de 60º. Expresa esta medida en radianes.
Paso 1: Comprendo el
problema
·
Datos: La medida del ángulo es 60º
·
Pregunta: ¿Cuál es la medida del ángulo en
radianes?
Problema 2: Analiza la resolución del siguiente problema
El minutero de un reloj al cabo de un tiempo se ha
desplazado 5/6
Paso 1: Comprendo el
problema
·
Datos: La medida del ángulo es 5/6
·
Pregunta: ¿Cuál es la medida del ángulo en
radianes?
v Transferencia
Actividad 3: Resolver el siguiente problema
Problema 1: Un yoyo al ser lanzado
verticalmente hacia abajo y sostenido por su cuerda, necesita girar 1.350º para
volver a impulsarse y subir. Expresa esta medida en radianes.
Problema 2: Una rueda gira sobre su propio eje
realizando una revolución de 7/4 𝜋
=================================================================================
GUIA # 2 MATEMATICAS PERIODO 1
|
GUÍA DE APRENDIZAJE N° 2 – PRIMER PERIODO |
|
|
Área: MATEMÁTICAS Asignatura: Matemáticas Grado: 10° Año: 2021 Docente: Juan Carlos Muñoz Castro Grupos: 10º 01, 10º 02, 10º 03 y
10º 04 Fecha de Inicio: 1 de marzo de 2021 Fecha Máxima de devolución: 19 de
marzo de 2021 |
|
|
Componente |
Espacial Métrico |
|
Tiempo |
Esta guía está diseñada para que la realices
en 3 semanas, dedicando 4 horas a
la semana |
|
Instrucciones para desarrollar la actividad |
Primero: Dedica un tiempo mínimo de una hora
cada semana a los saberes previos para su asimilación. Segundo: Dedica un tiempo mínimo de una hora
cada semana a la estructuración para su comprensión. Tercero: Dedica un tiempo mínimo de 2 horas
semanalmente a la transferencia para su desarrollo. Cuarto: Sí, tienes dudas o inquietudes en la
estructuración o en las actividades, consulta
al docente de la asignatura de tu grupo en el horario de comunicación semanal
con el docente atraves de llamada telefónica o video llamada. |
|
Recomendaciones |
Las actividades de transferencias se deben realizar en el cuaderno de
matemáticas. Al comienzo de cada actividad de transferencia debe tener el siguiente
encabezado: Nombre completo del estudiante, tema de la actividad, curso, periodo y
nombre del docente al que le envía. Si las actividades que envías no tienen
el encabezado, la actividad será devuelta. Enumera secuencialmente cada hoja
de la actividad En los videos que debas enviar debes de salir con el uniforme de
diario de la institución |
|
Medio de entrega |
Deben enviarlo al WhatsApp del docente de su grupo Juan Carlos Muñoz Castro: WhatsApp: 304 668 40 19 |
|
Productos a entregar por el estudiante |
Fotografías
de las actividades de transferencias
resuelta en el cuaderno de
matemáticas Un video donde expliques una de las actividades
de transferencias de la guía |
|
Hora de comunicación semanal con el docente |
Juan Carlos Muñoz Castro Grupo 10º 01
jueves de 7:00 a.m. a 9:00 a.m. Grupo 10º 02
miércoles de 7:00 a.m. a 9:00 a.m. Grupo 10º 03
viernes de 7:00 a.m. a 9:00 a.m. Grupo 10º 04
jueves de 9:00 a.m. a 11:00 a.m. |
Primera Semana: Perímetro y
Área
v
Saberes
Previos
Ø La Longitud: Es un atributo de los objetos, que se mide en una sola dimensión. Por
ejemplo, el largo, el ancho, el alto y la distancia entre dos puntos, son
longitudes.
Ø Unidades de longitud: La principal unidad de longitud en el Sistema Métrico Decimal es el metro (m). A partir del metro se definen otras unidades mayores que se
denominan múltiplos del metro, y otras unidades menores que se denominan
submúltiplo del metro, cuya equivalencia se muestra en la siguiente tabla.
|
Múltiplos |
|
Submúltiplos |
||||
|
Nombre |
Símbolo |
Equivalencia |
|
Nombre |
Símbolo |
Equivalencia |
|
Kilómetro |
Km |
1.000
m |
|
Decímetro |
dm |
0,1
m |
|
Hectómetro |
Hm |
100
m |
|
Centímetro |
cm |
0,01
m |
|
Decámetro |
Dm |
10
m |
|
Milímetro |
mm |
0,001
m |
Ø El Perímetro: El perímetro de una figura plana es la suma de las medidas de todos
sus lados.
Ø El Área: Es la medida de la región o superficie encerrada por una figura
geométrica plana. Para medir el área se utilizan unidades cuadradas.
Ø Unidades de Superficie: La principal unidad de longitud en el Sistema Métrico Decimal es el metro cuadrado (m2). A
partir del metro cuadrado se definen otras unidades mayores que se denominan
múltiplos del metro cuadrado, y otras unidades menores que se denominan
submúltiplo del metro cuadrado, cuya equivalencia se muestra en la siguiente
tabla.
|
Múltiplos |
|
Submúltiplos |
||||
|
Nombre |
Símbolo |
Equivalencia |
|
Nombre |
Símbolo |
Equivalencia |
|
Kilómetro
cuadrado |
Km2 |
1.000.000
m2 |
|
Decímetro
cuadrado |
dm2 |
0,01
m2 |
|
Hectómetro
cuadrado |
Hm2 |
10.000
m2 |
|
Centímetro
cuadrado |
cm2 |
0,0001
m2 |
|
Decámetro
cuadrado |
Dm2 |
100
m2 |
|
Milímetro
cuadrado |
mm2 |
0,000001
m2 |
Ø Fórmulas de Perímetro y Áreas
de Figuras Plana
v
Estructuración
Analiza la
resolución del siguiente problema
Desde una montaña se observa un terreno dividido en tres lotes con diferentes plantaciones. ¿Cuántos metros de alambre se necesita para cercar cada lote con tres hileras? y ¿Cuál es el área total del lote?
Paso 1: Comprendo el problema
·
Datos: La medida del lote destinado a plantar
aguacate es 50 m. Las medidas de los
lados del lote destinado a plantar uvas son 50 m y 60 m. Las medidas
de los lados del lote destinado a plantar papayas son 60 m, 40 m, 90 m y 50 m.
·
Preguntas: ¿Cuántos metros de alambre se
necesita para cercar el terreno con tres hileras? y ¿Cuál es el área total del
lote?
Paso 2: Elabora un
plan y lo llevo a cabo
Se calcula el perímetro del terreno para poder determinar cuántos metros de alambre se necesitan
Primero calculamos el
perímetro del terreno
Pt = L1 + L2 + L3 +
L4 + L5 + L6
Pt = 60 m + 50 m + 40
m + 90 m + 50 m + 50 m
Pt = 340 m
Segundo multiplicamos el perímetro del terreno por el número de hileras
Se calcula el área
de cada lote para determinar el área total del terreno.
v
Transferencia
Actividad 1: Resolver el siguiente problema
En construcción se utiliza un tipo de ventana formada por un rectángulo y un trapecio, como se muestra en la figura. Si la altura del trapecio es 2 m. ¿Cuál es el perímetro y el área de la ventana?
Segunda Semana: Volumen
v Saberes Previos
Ø Volumen: Es la medida del espacio que ocupa un cuerpo.
Ø Unidades de Volumen: La principal unidad de
volumen en el Sistema Métrico Decimal es el metro cúbico (m3). A partir del metro cúbico se definen
otras unidades mayores que se denominan múltiplos del metro cúbico, y otras
unidades menores que se denominan submúltiplo del metro cúbico, cuya
equivalencia se muestra en la siguiente tabla.
|
Múltiplos |
|
Submúltiplos |
||||
|
Nombre |
Símbolo |
Equivalencia |
|
Nombre |
Símbolo |
Equivalencia |
|
Kilómetro
cúbico |
Km3 |
1.000.000.000
m2 |
|
Decímetro
cúbico |
dm3 |
0,001
m2 |
|
Hectómetro
cúbico |
Hm3 |
1.000.000
m2 |
|
Centímetro
cúbico |
cm3 |
0,000001
m2 |
|
Decámetro
cúbico |
Dm3 |
1.000
m2 |
|
Milímetro
cúbico |
mm3 |
0,000000001
m2 |
Ø Fórmulas de Volumen de
Cuerpos Geométricos
v Estructuración
Analiza la resolución del siguiente problema
Cierto tipo de cereal viene en cajas cuyas dimensiones se muestran en la figura. Determina cuál es la presentación que resulta más económica por centímetro cúbico
Paso 1: Comprendo el
problema
·
Datos: Las dimensiones del cereal pequeño son
largo 10 cm, ancho 3,5 cm y alto 15 cm y las dimensiones del cereal grande son
largo 12 cm, ancho 5,5 cm y alto 20 cm.
·
Preguntas: ¿Cuál es la presentación más
económica por centímetro cúbico?
Paso 2: Elabora un
plan y lo llevo a cabo
Se calcula el volumen
de cada caja de cereal
·
Como la piscina tiene forma de paralelepípedo, el volumen se calcula así:
Volumen de la caja pequeña: V = l * a * h =
10 cm * 3,5 cm * 15 cm = 525 cm3
Volumen de la caja grande: V = l * a * h = 12
cm * 5,5 cm * 20 cm = 1.320 cm3
Se determina el valor por centímetro cúbico de cada caja
de cereales dividiendo el precio de la caja entre la cantidad de centímetros
cúbicos:
·
Caja pequeña: $ 7.500 ÷ 525 = $
14,3 por cm3
·
Caja grande: $ 22.000 ÷ 1.320 = $
16,7 por cm3
La caja más económica por centímetro cúbico es la pequeña.
v Transferencia
·
Actividad 2: Resolver el siguiente problema
La figura muestra las dimensiones de un contenedor y de las cajas que se van a almacenar en el contenedor.
Determina la cantidad de cajas que se pueden almacenar en el contenedor de tal forma que este quede totalmente lleno.
Tercera Semana: Capacidad
v Saberes Previos
Ø Capacidad: Es la medida de la cantidad de líquido que puede contener
un recipiente. La unidad básica para medir la capacidad en el Sistema Métrico Decimal es el litro,
que se simboliza como l. A partir
del litro se definen otras unidades mayores que se denominan múltiplos del
litro, y otras unidades menores que se denominan submúltiplo del litro, cuya
equivalencia se muestra en la siguiente tabla.
|
Múltiplos |
|
Submúltiplos |
||||
|
Nombre |
Símbolo |
Equivalencia |
|
Nombre |
Símbolo |
Equivalencia |
|
Kilolitro |
Kl |
1.000
l |
|
Decilitro |
dl |
0,1
l |
|
Hectolitro |
Hl |
100
l |
|
Centilitro |
cl |
0,01
l |
|
Decalitro |
Dl |
10
l |
|
Mililitro |
ml |
0,001
l |
Ø Equivalencia
Entre Capacidad y Volumen:
|
Capacidad |
|
Volumen |
|
1 Kilolitro (1 kl) |
= |
1 metro cubico (1 m3) |
|
1 Litro (1 l) |
= |
1 Decímetro cubico (1 dm3) |
|
1 Mililitro (1 ml) |
= |
1 Centímetro cubico (1 cm3) |
v Estructuración
Analiza la
resolución del siguiente problema.
Laura quiere construir una piscina en el patio de su casa, como la de la figura. ¿Cuál es el volumen y la capacidad de la piscina en litros?
Paso 1: Comprendo el
problema
·
Datos: Las medidas de la piscina son largo 12
m, ancho 9 m y profundidad 2 m.
·
Preguntas: ¿Cuál es el volumen y la capacidad
de la piscina en litros?
Paso 2: Elabora un plan y lo llevo a cabo
Se calcula el volumen de la piscina y su capacidad en
litros
·
Como la piscina tiene forma de paralelepípedo, el volumen se calcula así:
V = l * a * h = 12 m * 9 m * 2 m = 216 m3
·
Para calcular la capacidad de la
piscina en litros utilizamos la equivalencia 1 litro = 1 decímetro cubico, pero
como el volumen esta en metros cúbicos lo convertimos a decímetros cúbicos.
Como pasamos de metro cúbico a decímetro cúbico
multiplicamos por mil el volumen, o sea:
216 m3 = 216 * 1.000 dm3
= 216.000 dm3
Como 1 l = 1 dm3 entonces la
capacidad de la piscina en litros es 216.000 litros
v Transferencia
Actividad 3: Resolver el siguiente problema.
María mando a realizar un cajón como el de la figura, y desea saber ¿cuál es el volumen y la capacidad de este?
GUÍA # 1 MATEMATICAS PERIODO 1
|
GUÍA DE APRENDIZAJE N° 1 – PRIMER PERIODO |
|
|
Área: MATEMÁTICAS Asignatura: Matemáticas Grado: 10° Año: 2021 Docente: Juan Carlos Muñoz Castro Grupos: 10º 01, 10º 02, 10º 03 y
10º 04 Fecha de Inicio: 8 de febrero de 2021 Fecha Máxima de devolución: 26 de
febrero de 2021 |
|
|
Componente |
Aleatorio. |
|
Competencia 1 |
Comunicación. |
|
Aprendizaje 1 |
Reconocer la media, mediana y moda con base en la
representación de un conjunto de datos. |
|
Evidencia 1 |
Reconocer medidas de tendencia central en un
conjuntos de datos. |
|
|
|
|
Competencia 2 |
Razonamiento |
|
Aprendizaje 2 |
Formular inferencia y justificar razonamientos y
conclusiones a partir del análisis de información estadística. |
|
Evidencia 2 |
Formular conjetura sobre el comportamiento de una
población de acuerdo con los resultados relativos a una muestra de la misma. |
|
|
|
|
Competencia 3 |
Resolución
de Problemas |
|
Aprendizaje 3 |
Resolver y formular problemas a partir de un
conjunto de datos presentados en tablas, diagrama de barras y diagrama
circular. |
|
Evidencia 3 |
Usar información presentada en tablas y gráficas
para solucionar problemas en contexto cotidianos o de otras áreas. |
|
|
|
|
Tiempo |
Esta guía está diseñada para que la realices
en 3 semanas, dedicando 4 horas a
la semana |
|
Instrucciones para desarrollar la actividad |
Primero: Dedica un tiempo mínimo de una hora
cada semana a los saberes previos para su asimilación. Segundo: Dedica un tiempo mínimo de una hora
cada semana a la estructuración para su comprensión. Tercero: Dedica un tiempo mínimo de 2 horas
semanalmente a la transferencia para su desarrollo. Cuarto: Sí, tienes dudas o inquietudes en la
estructuración o en las actividades, consulta
al docente de la asignatura de tu grupo en el horario de comunicación semanal
con el docente atraves de llamada telefónica o video llamada. |
|
Recomendaciones |
Las actividades de transferencias se deben realizar en el cuaderno de
matemáticas. Al comienzo de cada actividad de transferencia debe tener el siguiente
encabezado: Nombre completo del estudiante, tema de la actividad, curso, periodo y
nombre del docente al que le envía. Si las actividades que envías no tienen
el encabezado, la actividad será devuelta. Enumera secuencialmente cada hoja
de la actividad En los videos que debas enviar debes de salir con el uniforme de
diario de la institución |
|
Medio de entrega |
Deben enviarlo al WhatsApp del docente de su grupo Juan Carlos Muñoz Castro: WhatsApp: 304 668 40 19 |
|
Productos a entregar por el estudiante |
Fotografías
de las actividades de transferencias
resuelta en el cuaderno de
matemáticas Un video donde expliques una de las actividades
de transferencias de la guía |
|
Hora de comunicación semanal con el docente |
Juan Carlos Muñoz Castro Grupo 10º 01
jueves de 7:00 a.m. a 9:00 a.m. Grupo 10º 02
lunes de 9:00 a.m. a 11:00 a.m. Grupo 10º 03
jueves de 9:00 a.m. a 11:00 a.m. Grupo 10º 04
miércoles de 8:00 a.m. a 10:00 a.m. |
Primera Semana: Conceptos
Generales de Estadística
v
Saberes
Previos
Ø La Estadística: Es una ciencia casi tan antigua como la humanidad. Comprende el
conjunto de métodos, estrategias y procedimientos para recolectar, organizar y
analizar datos que se pueden observar en una población o en una muestra.
La estadística brinda herramientas para la toma de decisiones más acertadas en
la medicina, la economía, los negocios, el deporte y en muchas otras ciencias.
Podemos clasificar la Estadística en descriptiva, cuando los resultados del
análisis no pretenden ir más allá del conjunto de datos, e inferencial cuando el objetivo del estudio es derivar las
conclusiones obtenidas a un conjunto de datos más amplio.
·
Estadística descriptiva: se ocupa de tomar los
datos de un conjunto, organizarlos en tablas o gráficos y calcular unos números
que nos resumen el conjunto estudiado.
·
Estadística inferencial: se ocupa de elaborar
conclusiones para la población, partiendo de los resultados de una muestra y
del grado de fiabilidad de estas conclusiones.
Ø Población: Conjunto de individuos o elementos que cumplen ciertas propiedades y
entre los cuales se desea estudiar un determinado fenómeno. Normalmente es
demasiado grande para poder abarcarlo.
Ø Muestra: Es un grupo más pequeño tomado de la población, pero que permite
obtener la misma información. A cada uno de los elementos de la población o la
muestra se le denomina individuo.
Ø Variable: Es una característica de la población o de la muestra cuya medida puede cambiar de valor. Según su
naturaleza pueden ser cualitativa o cuantitativa.
·
Variable cualitativa es aquella que representa
cualidades, atributos o características no numéricas.
·
Variable cuantitativa es aquella
característica de la población o de la muestra que es posible representar
numéricamente. La variable cuantitativa puede ser discreta o continua.
o
Discreta: Sólo puede tomar valores de números
enteros.
o
Continua: Cuando la variable puede tomar
cualquier valor en un rango determinado.
Ø Dato: Es el valor de la variable asociada a un elemento de la población o de
la muestra.
v
Estructuración
Analiza la resolución del siguiente
problema
El profesor de educación física registro el tiempo de un grupo de
estudiantes de 9º demoran haciendo los ejercicios relacionados con una prueba
física. A continuación, se muestran los resultados. Determina:
a.
La población
b.
La muestra
c.
Tipo de Variable
d.
Qué tipo de estadística se utilizaría para
determinar la resistencia física del 9º
|
18 |
25 |
23 |
31 |
30 |
28 |
19 |
21 |
|
23 |
32 |
25 |
23 |
21 |
18 |
22 |
27 |
|
30 |
28 |
24 |
20 |
27 |
19 |
31 |
26 |
Respuestas
a.
La población son todos los estudiantes del grado noveno
b.
La muestra es el grupo de 24 estudiantes del grado noveno
c.
La Variable es cuantitativa discreta
d.
Se utilizaría la estadística
inferencial
v
Transferencia
Actividad
a.
Unir con flechas la columna de la
izquierda con el tipo de variable correspondiente en la columna de la derecha.
|
Sus respuestas corresponden a: ·
Cualidad ·
Característica ·
Gustos ·
Preferencia |
|
Variable
cuantitativa |
|
|
|
|
|
Sus respuestas corresponden a: ·
Números |
|
Variable
cualitativa |
b.
A continuación, encontrarán tres
situaciones, en los cuales se hacen preguntas y al lado de cada uno aparece una
posible respuesta. Clasifique dichas respuestas como variables cualitativas o
cuantitativas, de acurdo con sus conocimientos previos y la parte a
|
¿Cuál es la estatura de Jaime Respuesta: 1,66 m |
¿Qué tipo de variable es: |
|
|
|
|
¿Cuál es tu equipo favorito de
Colombia? Respuesta: Junior de
Barranquilla |
¿Qué tipo de variable es: |
|
|
|
|
¿Cuál es tu edad? Respuesta: 20 años |
¿Qué tipo de variable es: |
c.
Escribe 5 ejemplos de variable
cualitativa, 5 de variable cuantitativa discreta y 5 de variable cuantitativa
continua
|
Variable
cualitativa |
Variable
cuantitativa discreta |
Variable
cuantitativa continua |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Segunda Semana: Recolección
y Representación de Datos
v Saberes Previos
Ø Los datos de un estudio
estadístico se recolectan mediante formularios, encuestas, entrevistas u
observaciones directas, entre otros. Luego, se organizan en tablas que permiten
clasificar y resumir la información.
El número de veces que se repite un dato se
llama frecuencia.
Ø Tabla de Frecuencia:
es una herramienta que permite ordenar los datos de manera que se presentan numéricamente las características de la distribución de un
conjunto de datos o muestra. También permite la
realización de los gráficos o diagramas estadísticos de una forma más fácil.
Tenemos dos tipos de tablas
de frecuencias:
·
Tablas de frecuencias con
datos no agrupados.
·
Tablas de frecuencias con
datos agrupados.
Ø Elementos de una Tabla de Frecuencia:
·
Datos: son los diferentes valores que toma la variable
en el estudio.
·
Frecuencia absoluta (fi): es la cantidad de veces que aparece el valor
en el estudio. La sumatoria de las frecuencias absolutas es igual al número de
datos.
·
Frecuencia relativa (fr): es la fracción o proporción de elementos que
pertenecen a una clase o categoría. Se calcula dividiendo la frecuencia
absoluta entre el número de datos del estudio.
·
Frecuencia porcentual (f%): es el porcentaje de elementos que pertenecen
a una clase o categoría. Se puede calcular rápidamente multiplicando la
frecuencia relativa por 100%.
Ø Graficas Estadísticas: Las gráficas estadísticas nos permite
“familiarizarnos” con los datos que se han recopilado y resumido. Se
considera como una técnica inicial de análisis exploratorio
de datos que produce una representación visual. Las gráficas resultantes
revelan un patrón de comportamiento de la variable en estudio. Se ofrecen muchos
tipos de gráficos para describir el conjunto de datos. Dependiendo del tipo
de datos y lo que se quiera representar, se hará uso del método gráfico
más adecuado.
Ø Tipos de Gráficos: A continuación, mostraremos los tipos de gráficos
más utilizados:
·
Gráficos de Barra: El más conocido y utilizado de todos los tipos
de gráficos es el gráfico o diagrama de barras. En éste, se presentan los datos
en forma de barras contenidas en dos ejes cartesianos (coordenada y abscisa)
que indican los diferentes valores. El aspecto visual que nos indica los
datos es la longitud de dichas barras, no siendo importante su
grosor.
Para construir un diagrama de barra
se tiene en cuenta lo siguiente:
Se dibujan dos ejes coordenados.
En el eje horizontal se escriben las
clases de la variable
En el eje vertical se utiliza una
escala conveniente, la cual se usará para ubicar la frecuencia de cada clase.
Las barras deben tener el mismo ancho y la misma separación una con otra.
·
Diagrama Circular: El también muy habitual gráfico en forma de
“quesito”, en este caso la representación de los datos se lleva a cabo mediante
la división de un círculo en tantas partes como valores de la variable
investigada y teniendo cada parte un tamaño proporcional a su frecuencia dentro del
total de los datos. Cada sector va a representar un valor de la variable con la
que se trabaja.
Para construir un diagrama circular se tiene en cuenta lo siguiente: Dividimos 360º entre el total de datos.
Multiplicamos cada frecuencia absoluta por el valor obtenido anterior mente (ángulo para cada fi). En cada ángulo escribimos la frecuencia porcentual correspondiente (f%).
v Estructuración
Analiza la resolución del siguiente
problema
En una institucion educativa se va alquilar las togas para la
graduación de los estudiantes de 11º, para poder definir el color de éstas se
decide realizar un estudio estadístico; para tal fin se le pregunta a un grupo
de 40 estudiantes de 11º por su color favorito y se obtuvieron los siguientes
resultados. ¿Cuál debe ser el color de las togas que se van al quilar?
|
Negro |
Azul |
Blanco |
Azul |
Blanco |
Negro |
Rojo |
Rojo |
Azul |
Rojo |
|
Azul |
Blanco |
Negro |
Rojo |
Azul |
Rojo |
Azul |
Negro |
Blanco |
Azul |
|
Rojo |
Negro |
Azul |
Rojo |
Negro |
Blanco |
Blanco |
Azul |
Rojo |
Blanco |
|
Blanco |
Rojo |
Rojo |
Blanco |
Rojo |
Azul |
Negro |
Blanco |
Rojo |
Negro |
Paso 1: Comprende
el problema
Datos: Los colores favoritos de los estudiantes de 11º
Pregunta: ¿Cuál debe ser el color de la toga que se va alquilar?
Paso 2: Elabora un plan y llévalo a
cabo
Para poder tener mayor claridad sobre los datos obtenidos,
se registran en una tabla de frecuencia
|
Color |
fi |
fr |
f% |
|
Frecuencia absoluta (fi):
Cantidad de veces que se repite la variable Frecuencia Relativa (fr): Se
divide cada fi entre el total de
dato Ejemplo: 8 ÷ 40 =
0,20 Frecuencia Porcentual (f%): Se
multiplica la fr por 100% Ejemplo: 0,20 x 100% = 20% |
|
Negro |
8 |
0,20 |
20% |
||
|
Azul |
10 |
0,25 |
25% |
||
|
Rojo |
12 |
0,30 |
30% |
||
|
Blanco |
10 |
0,25 |
25% |
||
|
Total |
40 |
1 |
100% |
Paso 3: Verifica y
redacta la respuesta
Para comprobar lo obtenido se construirá un gráfico de
barra
|
|
Respuesta: Las togas
se deben alquilar de color rojo Porque en la tabla de
frecuencias es el color que tiene mayor fi, fr y f%, a de más en el diagrama
de barra es la barra más larga
|
v Transferencia
Utiliza uno de los siguientes temas: Deporte,
género musical, asignatura, peso o edad en años.
Para realizar un estudio estadístico,
donde formules una conjetura sobre el comportamiento de una población de
acuerdo con los resultados relativos a una muestra de la misma.
Para realizar la actividad utiliza:
·
Como guía: La estructuración
·
Como población: Los estudiantes
del bachillerato del inseya en tu corregimiento.
·
Como muestra: Entre 20 y 30
estudiantes del bachillerato del inseya en tu corregimiento
Tercera Semana: Medidas de
Tendencia Central
v Saberes Previos
Ø Medidas de Tendencia Central: Las medidas de tendencia central son medidas estadísticas que pretenden
resumir en un solo valor a un conjunto de valores. Representan un centro en
torno al cual se encuentra ubicado el conjunto de los datos. Las medidas de
tendencia central más utilizadas son: media, mediana y moda.
Ø Moda (mo): En un grupo de datos es el dato que se presenta con mayor
frecuencia o que se repite más.
·
Cuando en un conjunto hay dos datos con una frecuencia alta, se dice que
es bimodal.
·
Cuando en un conjunto hay más de dos datos con frecuencias altas, se
dice que es polimodal.
·
Cuando en un conjunto de datos las frecuencias son todas iguales, se
dice que no hay moda
·
Cuando en un conjunto de datos las frecuencias son todas diferentes, se
dice que no hay moda.
Ø Mediana (me): En un grupo de datos ordenados de menor a mayor es el valor
que ocupa la posición central en caso
de tener un número impar de datos. Sí el grupo de datos es par, la mediana se
calcula sumando los dos valores centrales y dividiendo entre 2. Para determinar
la posición central se utiliza la siguiente formula (n + 1) ÷
2
Ø Media o Media Aritmética (x): Es el valor promedio
de un conjunto de datos numéricos, calculada como la suma del conjunto de
valores dividida entre el número total de valores.
v Estructuración
Analiza la resolución del siguiente
problema
A continuación, se presenta los datos correspondientes al tiempo
(en hora) que un grupo de estudiantes de 9º dedica a navegar en internet. ¿Calcula
las medidas de tendencia central?
|
3 |
5 |
5 |
5 |
8 |
5 |
7 |
4 |
8 |
7 |
|
4 |
8 |
3 |
7 |
5 |
4 |
5 |
4 |
6 |
6 |
|
6 |
5 |
5 |
4 |
5 |
6 |
4 |
6 |
3 |
6 |
Paso 1: Comprende
el problema
Datos: Tiempo (en hora) que un grupo de estudiantes de 9º dedican a navegar
en internet
Pregunta: ¿Calcular las medidas de tendencias central?
Paso 2: Elabora un plan y llévalo a
cabo
Para poder tener mayor claridad sobre los datos
obtenidos, se registran en una tabla de frecuencia
|
Horas |
fi |
fr |
f% |
|
Para determinar la moda miramos en la tabla cual es el
dato que tiene mayor frecuencia, este es 5 hora. Para determinar la mediana, teniendo en cuenta que la
cantidad de dato es par, se
calcula el promedio entre los dos datos centrales 15 y 16, los cuales
corresponden a 5 hora y 5 hora, por lo tanto, la mediana es 5 horas Para determinar la media realizamos lo siguiente: X =
((3x3)+(4x6)+(5x9)+(6x6)+(7x3)+(8x3)) ÷ 30 = 5,3 |
|
3 |
3 |
0,10 |
10% |
||
|
4 |
6 |
0,20 |
20% |
||
|
5 |
9 |
0,30 |
30% |
||
|
6 |
6 |
0,20 |
20% |
||
|
7 |
3 |
0,10 |
10% |
||
|
8 |
3 |
0,10 |
10% |
||
|
Total |
30 |
1 |
100% |
Paso 3: Verifica y
redacta la respuesta
Para comprobar lo obtenido se construirá un gráfico de
barra
 Respuesta
Respuesta
La moda es 5
horas
La mediana es
5 horas
La media es
5,3 horas
v Transferencia
Utiliza uno de los siguientes temas: Peso,
estatura, tiempo dedicado al estudio diariamente, edad en años y número de
hermanos.
Plantea una situación problema donde
tengas que halar las medidas de tendencia central.
Para realizar la actividad utiliza:
·
Como guía: La estructuración
·
Como población: Los estudiantes
del bachillerato del inseya en tu corregimiento.
·
Como muestra: Entre 20 y 30
estudiantes del bachillerato del inseya en tu corregimiento

























Comentarios
Publicar un comentario